Sqaska

Kuratowski's free set theorem, named after Kazimierz Kuratowski, is a result of set theory, an area of mathematics. It is a result which has been largely forgotten for almost 50 years, but has been applied recently in solving several lattice theory problems.
Denote by [X] ^{< ω} the set of all finite subsets of a set X. Likewise, for a positive integer n, denote by [X]ⁿ the set of all n-elements subsets of X. For a mapping , we say that a subset U of X is free (with respect to Φ), if 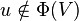, for any n-element subset V of U and any 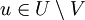. Kuratowski published in 1951 the following result, which characterizes the infinite cardinals of the form .
The theorem states the following. Let n be a positive integer and let X be a set. Then the cardinality of X is greater than or equal to if and only if for every mapping Φ from [X]ⁿ to [X] ^{< ω}, there exists an (n + 1)-element free subset of X with respect to Φ.
For n = 1, Kuratowski's free set theorem is superseded by Hajnal's set mapping theorem.